由大量微观粒子组成的系统，在宏观上服从不同的统计分布规律。自然界中的量子物质存在两种微观粒子，一种是玻色子，满足玻色-爱因斯坦统计，另一种是费米子，满足费米-狄拉克统计。然而，对于相互作用的量子体系，玻色-爱因斯坦统计及费米-狄拉克统计并不是仅有的量子统计形式，比如二维电子气体中可以涌现出分数化量子统计，即任意子（anyon）统计。1991年，著名物理学家、诺贝尔物理学奖得主F. D. M. Haldane提出了分数量子统计（Fractional Exclusion Statistics）的概念，并指出这是一种广义的量子统计规律，而玻色和费米分布是该分数统计规律的两种极限情况；1994年，著名华人物理学家吴咏时教授等研究了满足分数统计的理想粒子的热力学性质；此后，分数量子统计理论被用于分数量子霍尔效应、量子气体、自旋模型、任意子等诸多量子多体问题的理论研究中。然而，在实际实验系统中如何观测到这种分数量子统计一直存在很大的挑战。

一维排斥相互作用的玻色气体近年来已经成为实验上研究量子多体物理的重要平台。上世纪90年代初，吴咏时与合作者也最早证实了一维相互作用玻色子在准动量空间可以被描述成满足互易的分数量子统计的理想气体。然而，不同准动量之间的耦合作用（互易性）导致很难得到可测量物理量与统计因子之间的直接关系。

近期，全国信誉第一的网投平台(中国)有限公司量子材料科学中心张熙博研究员等人发现，当一维和二维相互作用玻色气体处于量子临界区域时（图1a），准动量空间的耦合是相当局域化的，恰恰表现出非互易的分数量子统计规律（图1b）；在一维和二维玻色体系的相变点附近，分数统计因子与相互作用强度之间存在非常简单的变换关系，并通过理论计算证实可测量物理量，如单粒子临界熵与分数统计因子满足简洁的幂律标度规律；更进一步地观察到相互作用玻色气体的更多热力学性质可以由满足分数量子统计的理想粒子给出，这个结果同时得到量子蒙特卡洛模拟研究和超冷原子实验数据的一致支持。

该研究成果不仅为观测分数量子统计提供了理论方法和数值与实验证据，而且为理解更加复杂的量子多体系统的临界行为提供了新的视野和方法，如具有高对称性的玻色和费米气体等。

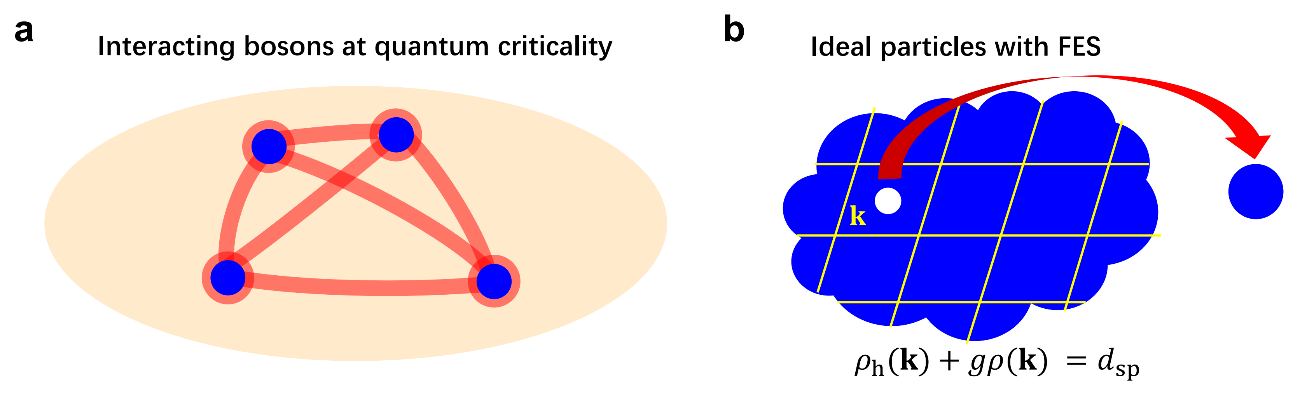
图1 临界物质与分数量子统计。（a）量子临界区域的相互作用玻色气体；（b）满足分数量子统计的理想粒子。

2022年2月24日，该工作以“相互作用诱导的粒子-空穴对称性破缺和分数量子统计”（Interaction-induced particle-hole symmetry breaking and fractional exclusion statistics）为题，在线发表于《国家科学评论》（National Science Review）。张熙博研究员为第一作者和通讯作者；合作研究者包括中国科学院武汉物理与数学研究所管习文研究员、陈洋洋博士，中国科学技术大学邓友金教授、刘龙祥博士。

上述研究工作得到国家重点研发计划、国家自然科学基金、科技创新2030—“量子通信与量子计算机”重大项目、中国科学院战略性先导科技专项，及量子物质科学协同创新中心、北京量子科学研究院、合肥国家实验室等支持。

论文原文链接：

https://academic.oup.com/nsr/advance-article/doi/10.1093/nsr/nwac027/6535630